Ocean Hemisphere Project

平成１１年度の研究成果

データ処理解析研究班（第４班）

"Direct Solution Methodを用いた３次元地球内部構造推定の進展"へ

　４班の最も大きな柱はデータセンターである。海半球ネットワークデータセンター（OHPDMC， http://ohpdmc.eri.u-tokyo.ac.jp）では、平成11年度までに海半球ネットワークで集められた地震波形データと、IRISイベントデータ、及び国内の地震ネットワークからの広帯域波形データを公開する体制を整備した。これには、気象庁の広帯域地震観測網、TPC-1の海底ケーブル広帯域地震波形データ、地震研究所の地震地殻変動観測センターの広帯域地震観測網データが含まれる。これら観測網のデータについては、個々の観測網のデータフォーマットを気にすることなく、全て国際標準フォーマット（SEED）で入手することができるシステムを整備した。海半球観測網のデータと併せて、日本の様々な機関の広帯域地震記録が世界的に広く活用されることを期待するものである。なお、上記システムはJava-RMIというネットワーク指向のプログラミングを用いて運用されており、何れのデータセンターもJava-RMIサーバを置くだけで同様のシステムを運用することが可能となる。この点及びより最近の発展については、別項の「パーソナル地震波形データ収集ツールNINJA」を参照して頂きたい。図１及び表１はそれぞれ海半球観測網の観測点分布、及びそれら観測点のデータが現在どこまで公開されているかを示したものである。
　データセンターではデータの公開と共に、Direct Solution Method（DSM）による地震波形の計算方法の開発を進めている。手法的に完成し実用化された部分から随時、地震波形計算ソフトウエアパッケージとして公開している。現在、こうした研究がどこまで進んでいるかを、竹内希氏に報告してもらう。
　その他４班の活動は多岐に渡るが、ここでは今年３月、雑誌SCIENCEに発表され毎日新聞（平成12年４月17日）でも報道された「固体地球と大気との共鳴振動」現象の発見について、西田究氏に報告してもらう。

Direct Solution Methodを用いた３次元地球内部構造推定の進展

　　　　　　　　　　　　　　　　竹内　希（東京大学地震研究所）

　地震波形データの解析を通じて、地震学的な３次元地球内部構造が推定できる。海半球ネットワーク計画では、観測と理論の両面から、こうして得られる地球内部構造モデルの精度と解像度の改善を行っている。観測の面では、これまで観測点密度が希薄であった地域に広帯域観測網を設置し、蓄積される地震波形データの質・量を改善している。一方理論の面でも、地震波形データをより洗練された方法で解析することにより、新たな地球内部構造に対する知見を得る試みがなされている。ここでは、理論研究の一部として行われている広帯域波形データの波形インバージョンの試みについての最近の進展について紹介する。
　波形インバージョンとは、地震波形データと理論波形を直接比較することによりモデルパラメータ（この場合は内部構造）を推定する手法であり、波形データに含まれるすべての情報を用いるため、より高解像度の地球内部構造モデルが推定できると期待されている。
しかし理論波形とその偏微分係数の計算量が膨大であるため、これらを高精度かつ効率的に計算することが必要不可欠である。我々は、波形インバージョンのための高精度かつ効率的な理論波形計算手法（Direct Solution Method; DSM）を開発し、1997年の海半球ネットワークニュースレター No.1 にて報告した。ここでは、主に1999年度に実施したDSM の実データへの応用の試みについて述べる。
　これまでの広帯域波形インバージョンでは、インバージョンのデータセット作成の際に、適当な前処理（実体波部分・表面波部分に分けて別のフィルターを施す、S や SS 等の特定のフェーズのみを抽出してデータとする等）を実施することが一般的であった。また計算時間の短縮のため、偏微分係数の計算に近似を用いていた。本研究の最終目標は、使える限りのデータを正確な計算に基づいて波形インバージョンすることである。そこで、フェーズの区別を一切せず、データと理論波形との残差がある一定レベルを越えない時間ウィンドウを選び出し、そのウィンドウ内のデータを機械的にすべてデータセットとした。これにより表面波が到達した後の実体波や、比較的短周期の表面波もデータとして活用している。また偏微分係数計算に近似を用いず、正確に計算を行った。
　インバージョンを実施する際、非球対称構造とともに球対称構造もモデルパラメータとした。これは正確なモデル推定の必要条件と考えられる。データと様々な球対称モデルに対して計算された理論波形との比較を図２に示す。

図２　97/11/8 のチベット地震（Mw = 7.5）に対する観測点BJT のトランスバース成分のデータと、各種球対称地球モデルに対して計算された理論波形との比較。100 - 400 s のバンドパスフィルターを施してある。

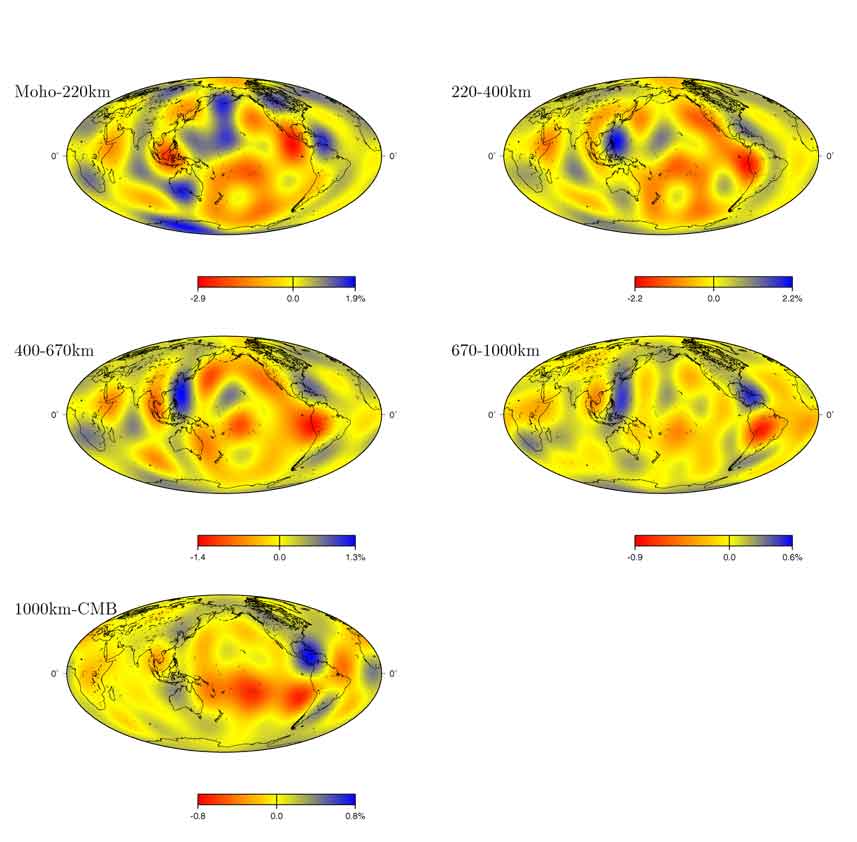
G2やG3の到達時刻が早いか遅いかは球対称モデル毎に異っている。これから、球対称構造を固定してしまうと、得られる不均質構造が与える球対称初期モデルに強く依存すると推察されるし、また事実そうなる。従って、球対称構造についてもインバージョンで補正を行うことが、本質的に重要である。初期モデルの選定には任意性があるが、ここでは anisotropic PREM を用いた。データと理論波形の残差は短周期表面波で最も大きくなるが、本初期モデルはそのデータを比較的よく説明し、その結果活用できるデータの量が多くなるという長所がある。
　以上のような方法により予備的な解析を実施した。５個の地震に対する781本の広帯域波形記録（周期50-400 s）のトランスバース成分をデータとして、degree-6 までの全マントルS波速度構造を求めた（図３）。モデルパラメータの数は196個である。基本的には過去の研究と整合的な結果が得られている。今後はデータを増やし、さらなる短波長構造を推定してゆく予定である。

図３　予備的な解析により得られた全マントルDegree-6 S波速度構造。球対称部分（degree-0）の摂動は除いてプロットしてある。

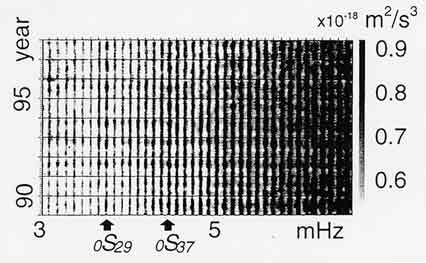
常時自由振動: 大気と固体地球の共鳴

　　　　　　　　　　　　　　　　西田究（東京大学地震研究所）

[始めに]
　ここ数年地球が常に自由振動している事が明らかになっててきた（e.g. Nawa et. al., 1998）。励起の特徴から地表付近の大気擾乱が自由振動を励起していると考えられている（Kobayashi and Nishida, 1998）。最近、大気励起を示唆する観測事実として、励起振幅の季節変動および大気と固体地球の“共鳴”が報告された（Nishida et. al., 2000, 図４参照）。ここでは主に共鳴について述べる。

図４　25観測点のスペクトログラムをスタックし、３カ月の窓で移動平均をとった図。以下二つの特徴がある。
（１）励起振幅の季節変動：図を見ると年変動に対応する変動を見てとれる。変動幅は振幅の10 %程度である。これらの変動の周期は１年であり、７月付近で極大値をとる。特に0S29の変動は顕著であり、変動幅は約40 %である。
（２）励起振幅の極大値：励起振幅は周波数が高くなるにつれ緩やかに大きくなり、２つの極大値（0S29, 0S37）を持つ。２つの極大値は大気との結合が強いモードに対応する。

[大気と固体地球の共鳴]
　観測された２つの余剰振幅は（図４参照）、固体地球のモードと大気が共鳴しているモードに対応する。ピナツボ火山の噴火時においても，これらのモードに対応する振動が観測された（Kanamori and Mori, 1992）。この２つの固体地球モードは大気と共鳴しているため、地表大気擾乱のみならず大気中の音波によって“余剰”に励起されているのである。余剰振幅の大きさから、大気ー固体地球の境界層付近における大気現象が励起源であると考えられる。

[チューニング・メカニズム]
　共鳴しているモードの季節変動は他のモードの変動より大きく（図４参照）、その変動の振幅は励起源の変動では説明できない。変動の大きさを説明するためには、大気は固体地球と違い密度や温度構造自体が年変動している事を考えなくてはならない。大気構造が変動するため大気音波の固有周期は変動し、大気音波と固体地球の固有周期の近さが変化する。共鳴の大きさもそれにともない変化する。結果として季節変動がより強調される。

[結論]
　余剰振幅は大気ー固体地球の共鳴の結果であり、その大きな季節変動は共鳴の変化で説明できる。今後は、大気・海洋・固体地球の相互の関係を考慮していく事がより重要になるだろう。

[文献]
K. Nawa, N. Suda, Y. Fukao, T. Sato, Y. Aoyama, 　and K. Shibuya, Earth, Planets and Space, 　　50 (1), 3-8, 1998.
N. Kobayashi and K. Nishida, Nature, 395, 　　　　357-360, 1998.
K. Nishida, N. Kobayashi, and Y. Fukao, Science, 　287, 2244-2246, 2000.
H. Kanamori and J. Mori, Geophys. Res. Lett., 19, 　721, 1992.

目次へ